반응형
출처 : http://blog.naver.com/alwaysneoi/100178956322
삼각함수 공식을 정확히 기억하고 있는가? 아마도 기억하고 있는 이는 많지 않아 보인다.
오늘은 이 지긋지긋한 삼각함수 공식을 확실하게 머리속에 넣어 두는 방법을 소개할까 하니 머리를 활짤 열고 준비하라.
간단하다. 쉽다. 오래 기억된다. ㅎㅎㅎ
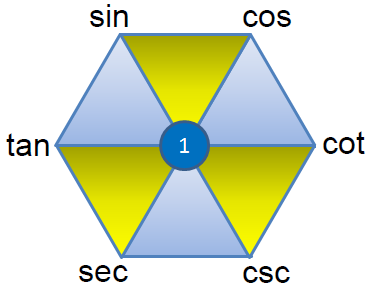
육각형을 그릴 줄만 알면, 32개의 삼각함수 공식을 32초만에 후딱 해치울 수 있다. 다음은 이 육각형을 그리는 방법이다.
| (1) 정육각형을 그린다. |
| (2) 왼쪽 위 귀퉁이에 우리에게 가장 친근한 sin을 적는다. |
| (3) 나머지 5개의 삼각함수를 sin을 기준, 시계 방향으로 알파벳 순서로 적는다. sin → cos → cot → csc → sec → tan |
| (4) 마지막으로 가운데에 1을 적는다. 준비 끝! |
★ 대각선 방향으로 놓여 있는 두 삼각함수는 역수 관계이다. 역수? 곱하면 1이라는 애기!
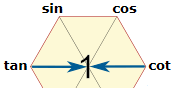
| (sin x)(csc x) = 1 | (cos x)(sec x) = 1 | (tan x)(cot x) = 1 |
★ 양 옆에 있는 두 삼각함수의 곱은 가운데에 있는 자신이다.
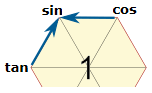
| sin x = (cos x)(tan x) | csc x = (cot x)(sec x) | cos x = (sin x)(cot x) |
| sec x = (csc x)(tan x) | cot x = (cos x)(csc x) | tan x = (sec x)(sin x) |
★ 연속하여 세 삼각함수가 있을 때, 두번째 함수를 세번째 함수로 나누면 첫번째 함수를 얻는다.
시계 방향과 시계 반대방향 모두!
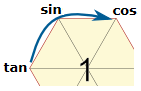
| sin x = (cos x)/(cot x) | sin x = (tan x)/(sec x) |
| cos x = (cot x)/(csc x) | cos x = (sin x)/(tan x) |
| cot x = (csc x)/(sec x) | cot x = (cos x)/(sin x) |
| csc x = (sec x)/(tan x) | csc x = (cot x)/(cos x) |
| sec x = (tan x)/(sin x) | sec x = (csc x)/(cot x) |
| tan x = (sin x)/(cos x) | tan x = (sec x)/(csc x) |
★ 한 칸을 건너 뛴 세 삼각함수의 곱은 1이다.
| (sin x)(cot x)(sec x) = 1 | (cos x)(csc x)(tan x) = 1 |
★ 3개의 색칠한 삼각형이 있다. 삼각형의 밑변의 양 꼭짓점에 있는 두 삼각함수의 제곱의 합은 아래에 있는 꼭짓점의 제곱과 같다.
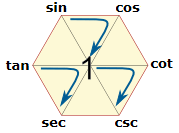
| sin² x + cos² x = 1 | tan² x + 1 = sec² x | 1 + cot² x = csc² x |
★ 3개의 열에 있는 두 삼각함수는 여각 관계이다. 여기서 여각이란 더하여 90°가 되는 두 각을 의미한다.
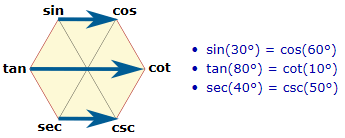
| sin(90° - x) = cos x | cos(90° - x) = sin x |
| tan(90° - x) = cot x | cot(90° - x) = tan x |
| sec(90° - x) = csc x | csc(90° - x) = sec x |
반응형
'정보생활 > 생활팁' 카테고리의 다른 글
| 냉동 만두 유통기한, 날짜 (0) | 2021.06.26 |
|---|---|
| 아이스크림 유통기한, 날짜 (0) | 2021.06.26 |
| 가족 관계 호칭 (0) | 2014.06.26 |
| '오' 와 '열' 을 아는가??? (0) | 2014.04.01 |
| 기계식 키보드 (0) | 2014.02.22 |



댓글